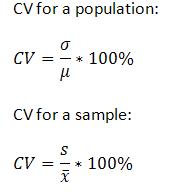Standard deviation basically means how much deviation is there in data set from its mean so you have idea about standard deviation and coefficient of variation but you want to know difference lets take a example and you will know why coef. Variance standard deviation and coefficient of variation.

Standard Deviation Index Sdi
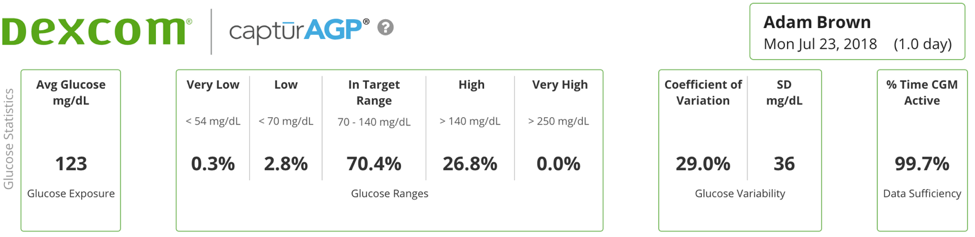
Cv versus standard deviation. Another way to describe the variation of a test is calculate the coefficient of variation or cv. Dividing the sd by the mean glucose and multiplying by 100 to get a percentage. Standard deviation is a measure of how much variation there is within a data setthis is important because in many situations people dont want to see a lot of variation people prefer consistent stable performance because its easier to plan around less riskyfor example lets say you are deciding between two companies to invest in that both have the same number of average. Terms dividing by n 1 and then taking the square root. On the other hand the standard deviation of the return measures deviations of individual returns form the mean. Thus sd is a measure of volatility and can be used as a risk measure for an investment.
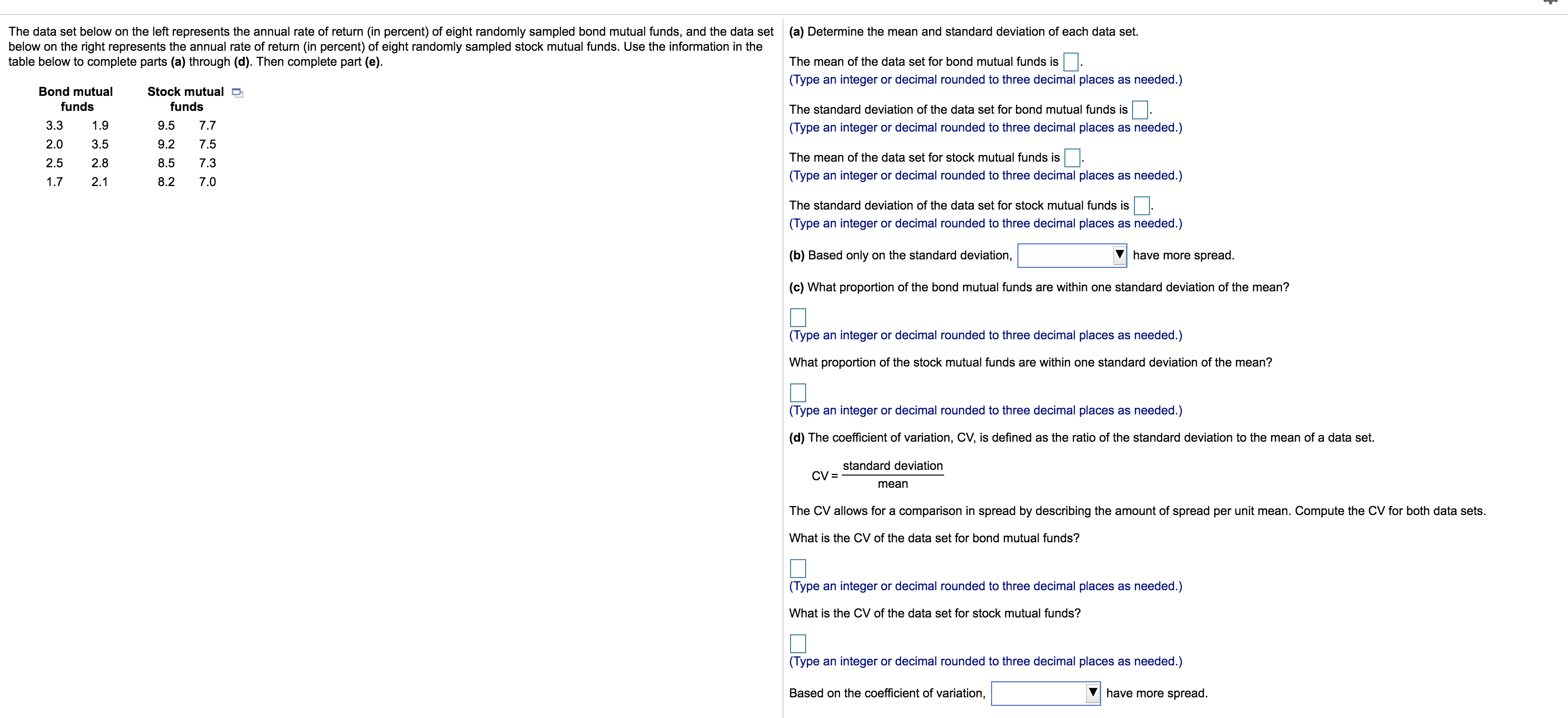
The cv expresses the variation as a percentage of the mean and is calculated as follows. This formula is saying that you calculate the standard deviation of a set of n numbers x i by subtracting the mean from each value to get the deviation d i of each value from the mean squaring each of these deviations adding up the. But a mean of 10 the std. The standard deviation is proportional to the mean eg. Coefficient of variation cv. If this is compared to the same std.
Coefficient of variation cv. Cv is a fancy term for a simple calculation. Standard deviation sd coefficient of variation cv. A coefficient of variation cv is a statistical measure of the dispersion of data points in a data series around the mean. Of 2 would correspond to 20. In the laboratory the cv is preferred when the sd increases in proportion to concentration.
1 it shows the extent of variability in relation to the mean of the population. The coefficient of variation should be computed only for data measured on a ratio scale that is scales that have a meaningful zero and hence allow relative comparison of two measurements ie division of one. A mean with 20 may have a std. This is almost identical to the formula for the root mean square deviation of the points from. The coefficient of variation cv is defined as the ratio of the standard deviation to the mean. In the field of statistics we typically use different formulas when working with population data and sample data.
However sd must be interpreted in context with the mean glucose which leads us to the third metric. It is calculated as follows. There are many ways to quantify variability however here we will focus on the most common ones.